-
로지스틱 회귀(logistic regression) in pythondata-science-summary/summary 2020. 9. 19. 15:57반응형
<엔지니어는 구현을 못하면 모르는것이다>
로지스틱 분류 LogisticRegression
일반 선형 회귀 모형 ax + b => 0과 1로 구분되는 데이터셋은 회귀분석으로는 힘듬
=> 오즈비를 활용한 ln(p/1-p) = ax+b => p = 시그모이드 함수
=> p 임계점에 따라 0과 1의 값으로 할당 가능
=> 즉 로지스틱 모델은 다양한 변수들을 종합하여 1,0 두가지로 확률을 예측하여 분류 하는 방법
오즈(Odds)란?
성공 확률이 실패 확률에 비해 몇 배 더 높은가를 나타냄

로짓(logit)이란?오즈 비에 로그를 씌운값

로지스틱 유도로짓과 회귀식의 연관성
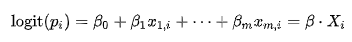
이런뒤 p를 기준으로 우변 정렬하면 로지스틱 펑션이 나옴

from sklearn import datasets from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split breast_cancer = datasets.load_breast_cancer() X = breast_cancer.data y = breast_cancer.target train_x, test_x, train_y, test_y = train_test_split(X, y, test_size=0.1, random_state=7777) train_y # C : Inverse of regularization, 절편없으면: fit_intercept=False lor = LogisticRegression(penalty='l2', C=100000, random_state=98709, solver='newton-cg') lor.fit(train_x, train_y) # 예측 preds = lor.predict(test_x) # 예측 확률 preds = lor.predict_proba(test_x) # logit 로짓 값들의 평균 # observation별 logit 값의 평균 # odds 는 실패에 비해 성공할 확률의 비 : p/(1-p) # odds 에 Log를 취한값이 바로 로짓 : Log(p) # 회귀분석의 y =ax +b 가 ln(p/1-p) = ax+b 가 된것 => 즉, 로지스틱 회귀분석은 일반회귀 함수를 로짓으로 변형한 분석법 import math import numpy as np arr = [] for pred in preds: # 만약에 아주 확률이 1에 가까워 1 이 나온다면 최대한 1보다 작은 가장 큰값 입력 arr.append(math.log(float(pred[1])/float(1-pred[1]))) print(np.mean(arr)) # 또는 print(np.mean(np.log(preds[:,1]/preds[:,0]))) # 가장 영향이 큰(기준: Odds Ratio) 독립변수 => e 의 지수에 해당 변수가 위치하므로 np.exp 를 사용한다. cols = breast_cancer.feature_names print(cols[np.exp(lor.coef_).argmax()]) # 변수에 대한 계수 lor.coef_ # 특정 변수에 대한 오즈비 => 로지스틱 회귀분석에서 오즈비는 np.exp(특정변수의 계수) np.exp(lor.coef_[0]) # 평균면적이 1 증가할때 마다 유방암에 걸릴 확률이 몇배나 증가한다고 할 수 있는지를 구하라 => mean area 에 대한 오즈비를 구하라(Odds Ratio) # 오즈비는 1증가할떄마다 얼마나 증가하는 지를 보인다. 만약 0,2가 값으로 있다면 minmax를 하는것이 좋고, 3가지 값이 있다면 one-hot encoder 후 학습시킨뒤 비를 구하면 더 정확함 i = cols.tolist().index('mean area') np.exp(lor.coef_[0][i]) # 예측확률에 따른 예측치 결정(threshold or cut off value) pred_pro = np.where(preds[:,1]>0.5, 1, 0) pred_pro반응형'data-science-summary > summary' 카테고리의 다른 글
one-hot encoding 하는법 in python (0) 2020.09.19 Logistic regression 에서 통계적으로유의한 독립변수 찾는법 in python (0) 2020.09.19 회귀 (연속형 변수) 측정하는법 MSE, RMSE, MAE, MPE, MAPE in python (1) 2020.09.18 VIF(Variance Inflation Factor) 분산팽창지수 in python (0) 2020.09.18 결정 계수 in python (0) 2020.09.17